Учебник CSS
Невозможно отучить людей изучать самые ненужные предметы.
Введение в CSS
Преимущества стилей
Добавления стилей
Типы носителей
Базовый синтаксис
Значения стилевых свойств
Селекторы тегов
Классы
CSS3
Надо знать обо всем понемножку, но все о немногом.
Идентификаторы
Контекстные селекторы
Соседние селекторы
Дочерние селекторы
Селекторы атрибутов
Универсальный селектор
Псевдоклассы
Псевдоэлементы
Кто умеет, тот делает. Кто не умеет, тот учит. Кто не умеет учить - становится деканом. (Т. Мартин)
Группирование
Наследование
Каскадирование
Валидация
Идентификаторы и классы
Написание эффективного кода
Самоучитель CSS
Вёрстка
Изображения
Текст
Цвет
Линии и рамки
Углы
Списки
Ссылки
Дизайны сайтов
Формы
Таблицы
CSS3
HTML5
Новости
Блог для вебмастеров
Новости мира Интернет
Сайтостроение
Ремонт и советы
Все новости
Справочник CSS
Справочник от А до Я
HTML, CSS, JavaScript
Афоризмы
Афоризмы о учёбе
Статьи об афоризмах
Все Афоризмы
| Помогли мы вам |
Физики рассказали, как готовить идеальные блинчики - «Интернет и связь»
Физики из Новой Зеландии и Франции разработали оптимальную стратегию поджаривания блинчика, при которой его поверхность получается наиболее плоской. Для этого ученые поставили и решили задачу оптимального управления, то есть составили уравнение движения теста и нашли траекторию, при которой однородность блина максимальна, а затрачиваемые усилия минимальны. Статья опубликована в Physical Review Fluids, пишет N+1.
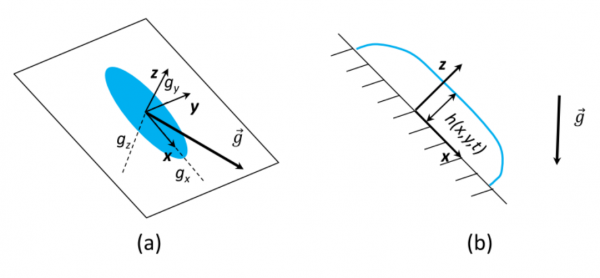
Физики Эдуард Бужо (Edouard Boujo) и Мэтью Селлиер (Mathieu Sellier) нашли оптимальные движения, с помощью которых можно выровнять блин (cr?pe). Для этого ученые переформулировали задачу выпекания блина как задачу оптимального управления. По словам физиков, до сих пор эту задачу никто толком не решал — как правило, при описании похожих процессов исследователи пренебрегают силой тяжести, тогда как при выпекании блинов она играет очень важную роль.
Сначала физики составили уравнение движение теста по поверхности сковороды, учитывая начальные условия (тесто выливается в центр сковороды) и граничные условия (положение стенок сковороды и температура ее дна). При этом исследователи учитывали изменение вязкости и плотности остывающего теста, силу тяжести и силу Кориолиса. Поэтому конечное уравнение движения сводилось к нелинейному параболическому дифференциальному уравнению.
Параметры этого уравнения (например, теплопроводность теста) ученые определили на глаз, численно моделируя динамику теста и сравнивая ее с приготовлением настоящих блинов. По словам авторов статьи, этот этап исследований понравился их дочерям больше всего.
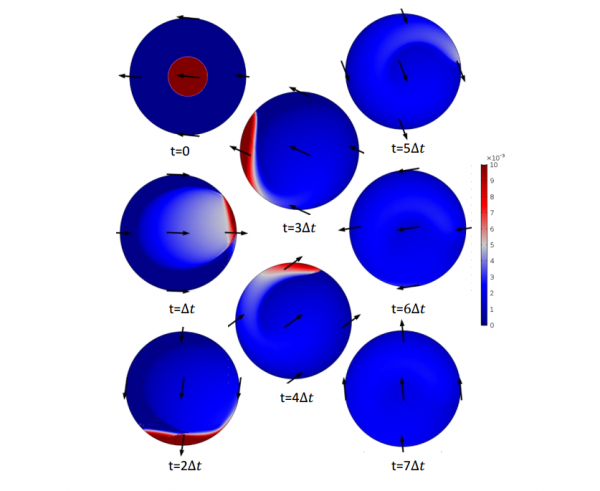
Затем исследователи попытались вслепую найти оптимальное движение, при котором толщина блина получается наиболее равномерной. Для этого ученые предположили, что вращательное и вертикальное движение сковороды представляют собой гармонические колебания с неизвестной амплитудой и периодом, и подобрали оптимальные значения параметров с помощью метода Монте-Карло. В результате физикам удалось на 40% улучшить однородность блина по сравнению с неконтролируемым выпеканием. Тем не менее, исследователи догадывались, что рассмотренные движения не являются оптимальными.
Поэтому ученые рассмотрели наиболее общие траектории выпекания блинов, которые допускают составленные дифференциальные уравнения. Для этого они составили объектную функцию, которая описывает отклонение формы блина от идеальной плоскости (точнее, идеально плоского цилиндра) и усилие, которые необходимо затратить на изменение формы.
Грубо говоря, усилие — это суммарное изменение угла и высоты центра масс сковороды, поэтому оно зависит от способа выпекания. Чтобы найти минимальное значение объектной функции на уравнениях движения, физики составили сопряженное уравнение и воспользовались методом градиентного спуска. Ученые подчеркивают, что этот способ не только более общий, но и гораздо менее затратный, чем поиск вслепую методом Монте-Карло. В конце концов, физикам удалось довести однородность блина до 180% от однородности неконтролируемого выпекания.
Учитывая проделанную работу, исследователи предлагают следующую стратегию выпекания блина. Первым делом налейте тесто в центр сковороды, наклоните ее примерно на 10 градусов и подождите, пока тесто не достигнет бортика. Затем покрутите наклоненную сковороду, чтобы тесто сделало полный круг и равномерно заполнило всю доступную площадь. Наконец, продолжая круговое движение, уменьшите наклон сковороды до нуля и подождите, пока идеальный блинчик не будет готов.
Читайте также
Семь самых коротких научных статей и очень необычное решение математической задачи
Одна рука с шестью пальцами может быть эффективнее двух с пятью
Ученые рассказали, что нужно есть вместо красного и переработанного мяса, чтобы жить дольше

Если вы заметили ошибку в тексте новости, пожалуйста, выделите её и нажмите Ctrl+Enter
- © 95% людей не могут решить эту задачу про яблоки и бананы. И вы тоже не сможете | - «Интернет и связь»
- © Физики рассчитали срок смерти Вселенной - «Интернет и связь»
- © Внутрь атома поместили другой атом - «Интернет и связь»
- © В центре науки "Элементо" пройдет бесплатная лекция "История физики" - «Интернет и связь»
- © Создана новая теория черных дыр | - «Интернет и связь»
- © Биологи описали "сверхорганизм" пчел - «Интернет и связь»
- © Физики создали новую форму света - «Интернет и связь»
- © Китайцы утверждают, что создали "невозможный" двигатель, нарушающий законы физики | - «Интернет и связь»
- © Акустическая левитация впервые подняла сантиметровый объект - «Интернет и связь»
|
|
|